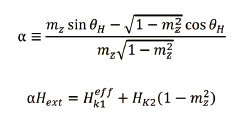터널자기접합 구동 위한 기술, 성능평가 기술 등

MRAM은 자성체를 활용한 비휘발성 메모리로써 실리콘 반도체 메모리를 이을 차세대 메모리로써 주목받고 있다.

MRAM을 상용화하기 위해서 현재 많은 기술들이 개발되었으며, 또한 이 기술들을 정량적으로 평가할 수 있는 여러 가지 방법들이 소개되어지고 있다. 이 글에서는 MRAM을 이끌어갈 기술들에 대해서 간략하게 설명하고자 한다.
 
글/ 고려대학교 주병권 교수 연구실
     주병권(고려대학교 전기전자공학부 교수)
     한동수(한국과학기술연구원 스핀융합연구단 선임연구원)
     장성현(한국과학기술연구원 스핀융합연구단, 고려대학교 전기전자공학과 석사 과정)


목차

개요 
1. 서론 
2. 자기저항 메모리 (Magnetoresistive Random Access Memory, MRAM)를 구동시키는 기술 소개 
2-1. 거대자기저항 (Giant Magnetoresistance, GMR) 2-2. 터널자기저항 (Tunneling Magnetoresistance, TMR) 
2-3. 라쉬바-에델슈타인 효과 (Rashba-Edelstein Effect) 
2-4. 전기장 제어 자기이방성 (Voltage Controlled Magnetic Anisotropy, VCMA) 
2-5. 자구벽 이동 (Domain Wall Motion) 
3. 신세대 기술 성능 평가 
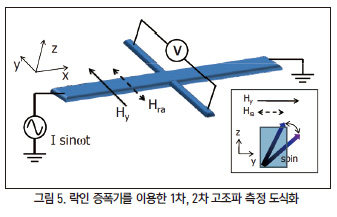
3-1. 락인 증폭기를 이용한 1차, 2차 고조파 측정 
3-2. 자기 이방성 평가 
4. 기술개발 현황 
5. 결론 
6. 참고문헌


1. 서론

최근 4차 산업혁명이 들어서기 시작 하면서 인공지능이 모든 산업에서 이용 되기 시작하였다, 당장 우리 주변을 보더 라도 개인의 취향에 맞게 영화나 음악을 추천하는 인공지능이 있을 정도로 인공 지능은 현재 우리 생활에 깊숙이 침투하고 있는 중이다. 이렇게 인공지능이 늘어 남과 동시에 인공지능이 다뤄야 할 정보의 양 또한 늘어나 메모리의 중요성도 또한 높아지고 있는 중이다.

메모리의 중요 도가 예전보다 높아지기 시작하면서 메모리의 성능을 높이려는 시도가 지속되 고 있지만, 2-3nm 수준의 공정이 개발된 현재, 실리콘 반도체만으로 메모리를 개발하는 것에는 한계를 느끼고 있는 중이다. 이러한 이유로 기업들은 실리콘 반도체 뿐만이 아니라 양자 컴퓨팅, 뉴로모픽 등을 이용하여 메모리의 성능을 개선 시키려는 노력들을 하고 있는 중이다.

그중에서도 자성체를 이용한 MRAM(Magnetic Random Access Memory)은 차세대 메모리로써 각광받고 있는데, MRAM은 기존 실리콘 반도체 메모리에 비해 전원이 없어도 데이터 보존이 가능하며 이로 인해 적은 전력만으로도 구동할 수 있다는 장점이 있다.

이러한 장점들을 인정받아 MRAM은 삼성전자 혹은 SK 하이닉스와 같은 국내 최대 반도체 기업에서 활발히 연구되고 있다. MRAM은 터널자기접합을 기반으로 셀을 구성하여 정보를 저장하는데, 이 터널자기접합을 구동하기 위해서는 고도의 기술 들이 필요하다. 터널자기접합을 더 효율적으로 구동하는 기술들은 거대자기저항부터 스핀전달토크, 스핀궤도토크 등을 거쳐 점점 진화되어 왔는데, 지금부터 그 기술들을 알아보고 그것들의 성능평가를 어떻게 진행하는지도 알아보자.
 
2. 자기저항 메모리(MRAM)를 구동시키는 기술 소개

2.1 거대자기저항 (GMR, Giant Magnetoresistance)

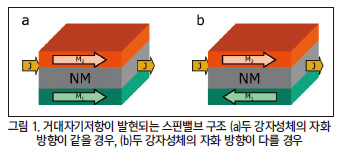
거대자기저항은 주로 강자성층 위에 비자성층을 쌓고 다시 그 위에 강자성층을 쌓은 스핀밸브 구조에서 주로 나타난다. 이스핀밸브 구조에 전류를 인가하게 되었을 때, 전자는 전자의 스핀 방향에 따라 산란되는 정도가 달라지는데, 이에 의해 강자성 층의 자화 방향에 따라 저항이 크게 차이가 나게 변한다.

만약 두 강자성층의 자화 방향이 같은 방향으로 나열되어 있을 경우는 전자의 산란이 적게 일어나 대부분의 전자들이 스핀밸브 구조를 통과할 수 있게 된다. 이는 곧 스핀밸브의 저항과 직결되 며, 두 강자성 층의 자화 방향이 평행할 때 스핀밸브의 저항이 낮아진다고 말할 수 있다. 그러나 두 강자성층의 자화 방향이 서로 반대 방향으로 나열되어 있을 경우에는 전자의 산란이 많이 일어나게 되어 일부의 전자들만이 스핀밸브 구조를 통과하게 된다.

이에 따라 두 강자성층의 자화 방향이 서로 반평행할 경우에는 스핀 밸브의 저항이 상승하게 된다. 이렇게 두 강자성층의 자화방향에 따라 저항이 차이나는 현상을 거대 자기저항이라고 정의한다. 그리고 이 2개의 상태의 저항 차이를 이용하여 메모리 로써 구현한 것이 하드디스크가 되겠다. 이 현상은 1988년에 알베르 페르(Albert Fert) 박사가 제일 처음 발견하였으며, 1997년에 스튜어트 파킨(Stuart Parkin) 박사가 스핀밸브를 통해 거대자 기저항을 구현하여 세계 최초로 거대자기저항 하드 디스크로 개발하는데 성공하였다. 그리고 2007년에 알베르 페르 박사는 이현상을 발견한 공로로 페터 그륀베르크(Peter Grünberg) 박사와 함께 노벨 물리학상을 공동 수상하였다.

2.2 터널자기저항(TMR, Tunneling Magnetoresistance)

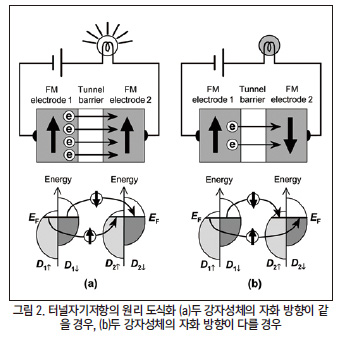
터널자기저항은 거대자기저항에서 더 발전된 형태로써 거대자기저항은 2개의 강자성체 층 사이에 비자성체 금속층이 들어가는 스핀 밸브 형태에서 나타나는 현상이라면, 터널자기 저항은 비자성체 금속층 대신에 절연체가 들어가는 터널자기 접합(Magnetic Tunneling Junction, MTJ)에서 주로 나타난다.

MTJ에서는 전자가 얇은 절연층을 터널링하여 다른 강자성층으로 들어가는데, 이때 전자가 터널링 확률은 페르미 준위와 상태 밀도에 영향을 크게 받는다. 여기에서 상태 밀도는 전자의 스핀에 따라 불균일하며, 이로 인해 전자가 스핀의 방향에 따라 터널링하는 빈도가 달라지게된다. 이에 따라 MTJ에서는 저항 차이가 발생하게 되며, 이 저항 차이를 이용하여 메모리로 구현한다. 터널자기저항에는 두가지 형태가 존재하는데, 2개의 강자성층의 보자력을 통해 터널자기저항을 제어하는 방식과, 1 개의 자성층의 자화 방향을 고정시켜놓고 다른 1개의 자성층의 자화 방향을 바꿔서 제어하는 방식이 존재한다.
 
2.3 라쉬바-에델슈타인 효과 (Rashba-Edelstein Effect)

스핀궤도결합이 강한 물질과 자성층을 접촉시켰을 때 두 물질간의 에너지 밴드 차이로 인해 전계가 형성되었을 때 여기에 전자가 지나가면 자기장이 발생하는 효과를 라쉬바-에델슈타인 효과라고 한다. 라쉬바-에델슈타인 효과로 인해 발생한 자기장은 그대로 자성층의 자화에 영향을 미쳐 토크를 인가하게 된다. 이렇게 토크를 자성층에 인가한다는 점에서는 스핀 홀효과와 맥락을 같이하나 스핀 홀 효과는 벌크에서 일어나고, 라쉬바-에델슈타인 효과는 두 물질 간의 계면에서 발생한다는 차이점이 존재한다.

2.4 전기장 제어 자기이방성(VCMA, Voltage Controlled Magnetic Anisotropy)

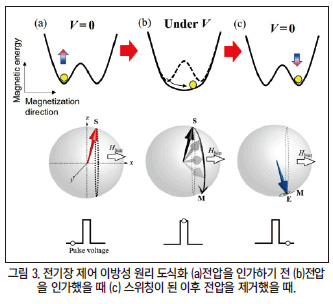
자성체에는 크게 두 가지 축이 존재하는데, 쉬운 자화 축과 어려운 자화 축이 그것이다. 이 두 가지 축은 말 그대로 자화가 되기 쉬운 방향과 자화가 되기 어려운 방향을 의미하는데, 이 두 축 사이에는 에너지의 차이가 존재하며 이 에너지의 차이 자기 이방성 에너지라고 정의한다.

자성체를 메모리로 구현 하기 위해서는 자성체의 자화 방향을 효율적으로 제어하는 것이 중요한데, 쉬운 자화 축으로 자화 방향이 고정되어있는 자성체에서 자화 방향을 180도 회전시켜 또 다른 쉬운 자화 축으로 자화 방향으로 고정시키는 것에는 방금 전의 자기 이방성 에너지로 인해 상대적으로 많은 에너지를 필요하게 된다. 이에 따라 효율적으로 자화 방향을 제어하기에는 어려워진다. 따라서 전기장을 인가하여 자기 이방성 에너지를 일시적으로 줄여줘 자화 방향을 바꾸는 것을 더 수월하게 할 수 있다.

전기장을 가해서 자기 이방성 에너지를 변화하는 방식에는 크게 2 가지가 존재한다. 먼저 첫 번째는 전기장을 인가하여 산화층과 자성층 사이의 전자 밀도를 바꾸어 자기 이방성 에너지를 변환하는 방식이 있으며, 그 다음으로는 산화층 내부의 산소이온을 이동시켜 자성층의 자기 이방성을 변환하는 방식이 존재한다.

전기장 제어 자기이방성은 스핀궤도토크 혹은 스핀 전달토크 등과 함께 차세대 자기 메모리를 이끌어 나갈 핵심기 술로써 평가받고 있으며, 최근에는 다른 기술과 결합하여 보다더 효율적으로 스위칭할 수 있는 메모리를 개발하는데 성공하기도 하였다. 그러나 이렇게 전기장 제어 자기이방성을 활용하는 기술에는 소자의 내구도가 떨어진다거나 높은 전압을 필요로 하는 등 한계점이 존재한다. 따라서 현재는 이런 한계점을 극복하려는 시도가 시행되고 있다.
 
2.5 자구벽 이동 (Domain Wall Motion)

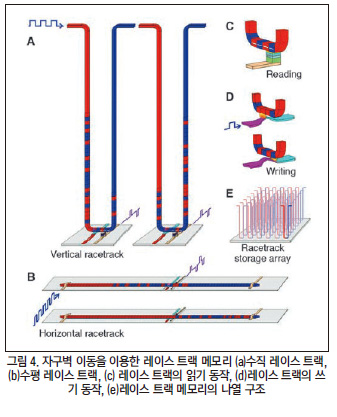
자구란 같은 자화 방향을 갖는 원자가 평행하게 배열된 영역을 의미하며, 자구벽은 이 자구를 구별짓는 공간이다. 자구벽을 이동시켜 자기적 특성을 평가하는 연구들은 예전에도 있어 왔으나, 자구벽의 이동을 메모리에 적용시킨 사례는 비교적 최근에 나타났다. 자구벽 이동을 이용한 메모리 중 제일 대표적인 사례가 2008년 스튜어트 파킨(Stuart Parkin) 박사가 개발한 레이스 트랙 메모리이다.

레이스 트랙 메모리는 특이하게 하드 웨어가 움직이는 것이 아닌 기록된 정보가 새로운 정보에 밀려서 이동하는 방식을 사용하고 있으며, 이러한 기술에는 자구벽 이동이 적용되고 있다. 레이스 트랙 메모리는 나노 와이어에 전자를 주입하는데, 이 주입된 전자는 스핀전이를 일으켜 자구의 자화 방향을 바꾸게 되며, 그에 따라 자구벽도 이동하게 되는 것이다. 이러한 원리로 작동되는 레이스 트랙 메모리는 타메모리들에 비해서 정지해 있기 때문에 내구도가 훨씬 좋으며, 고밀도로 정보를 저장할 수 있어 대용량 메모리에 적합하다는 장점을 가지고 있다.
 
3. 신세대 기술 성능 평가

3.1 락인 증폭기를 이용한 1차, 2차 고조파 측정

자기모멘트가 수직인 시스템에서 평면상으로 자기장을 인가 해주면 자화의 방향을 결정하는 자기모멘트는 자기장 방향을 따라서 수직에서 조금 떨어진 곳을 향하게 된다. 여기에서 낮은 주파수의 교류전류를 인가해주게 된다면 자기모멘트는 교류 전류의 주파수와 같은 주파수로 진동하게 된다.

이렇게 자기 모멘트가 진동함에 따라 자기저항 또한 변하게 되는데, 이는 노이즈를 제거하는데 사용되는 락인 증폭기(Lock-in Amplifier) 를 통해서 측정가능하다. 여기서 락인 증폭기는 교류전류를 인가하고 자기장의 크기 혹은 방향에 따라 변하는 자기저항의 1차 고조파, 2차 고조파를 측정하는데, 이를 분석하면 자기모멘트에 실질적으로 작용하는 유효 자기장의 크기를 알아낼 수 있다.
 
이 유효자기장의 크기는 자기장의 크기 혹은 방향에 따라서 변화하는데, 이는 곧 자기장에 따라 변하는 유효자기장으로써 스핀 궤도 토크의 크기와 직결이 된다. 이렇게 스핀궤도토크를 측정하는 방법은 기존의 핵형성을 이용한 방법보다 더 작은 크기의 자기장과 전류를 인가하여 측정할 수 있다는 이점이 존재한 다. 이렇게 스핀궤도토크를 측정하는 방법은 2010년 삼성종합 기술원의 피웅환 수석 연구원께서 처음 고안해내었으며, 현재 스핀궤도토크를 연구하는 수많은 연구자들이 스핀궤도토크를 측정하는 수많은 방식들 중에 가장 선호하는 방식이기도 하다.

현재는 피웅환 수석연구원님께서 고안하신 방식에서 자기장의 방향에 따라 자기저항이 달라지는 플래너 홀 효과(Planar Hall Effect, PHE)에 의한 영향, 그리고 전류와 자기장을 인가해줌에 따라 발생하는 열에 의한 영향 등이 추가되었으며 지금도 그 이외의 변수를 탐구하는 연구가 지속되고 있는 중이다.
 
3.2 자기이방성 평가

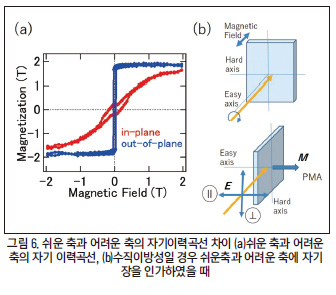
자성 물질의 자기이방성을 평가하는 방법에는 여러 가지 방법이 존재하는데 여기에서는 두 가지만 소개하려 한다. 첫 번째는 진동시료형 자력계(VSM, Vibrating Sample Magnetometer)에서 자화가 어려운 축의 자기이력곡선을 활용하는 방법이며, 두 번째는 자성체의 홀 저항을 측정하여 그로부터 자기이방성의 파라미터를 이끌어 내는 일반 석스미 스-톰슨 방법(General Sucksmith-Thompson method, GST method)이 그것이다.

먼저 첫 번째 방법부터 소개 하자면 진동시료형 자력계 측정을 할 때, 자성체가 자화되기 쉬운 방향과 어려운 방향에 따라서 자기이력곡선이 다른 형태로 그려지게 된다. 이때, 쉬운 축과 어려운 축의 자기이력 곡선에는 차이가 존재하게 된다. 이것은 자성체에 자기장을 인가해줬을 때 자성체에 발생 하는 포텐셜 에너지인 지만 에너지(Zeeman Energy)의 차이가 존재하기 때문이다.

여기에서 발생한 지만 에너지의 차이는 자기이방성 에너지에 의해 상쇄된 것으로 판단하며 따라서 두 방향에서의 자기이력곡 선에서의 차이를 자기이방성 에너지로 정의를 한다. 그리고이 자기이방성 에너지를 자성층의 두께로 나누어 주면 자성층 고유의 유효 자기 이방성 상수를 얻을 수 있다.
 
두 번째 방법은 홀 저항을 이용하는 방법인 일반 석스미스-톰슨 방법이다. 이 방법을 하기 위해서는 소자를 기준으로 수직선에서 각도를 기울여서 자기장을 인가한다. 여기서 수직선 으로부터 자기장 방향이 이루는 각도를 θ_H 로 정의한다. 이렇게 자기장을 인가하고 위에서 설명한 고조파 측정법을 진행하면 그에 따른 홀 전압을 얻을 수 있다. 이렇게 얻은 홀 전압을 정규화하면 코사인 형태의 함수가 도출되게 된다. 여기서 이 코사인 함수의 각도는 자화가 수직선과 이루는 각도이며 θ_M 으로 정의된다. 그리고 다음과 같이 수식을 전개한다.
 
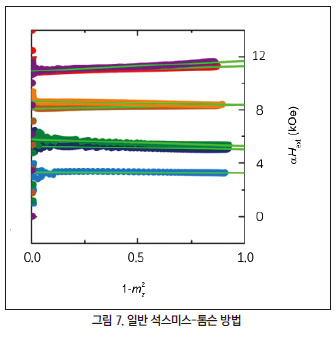
그리고 이 수식에서 1-m_z² 을 x축으로 αH_ext 를 y축으로 설정 하여 그래프를 그려 낸 다음 위의 수식에 적합화하면 그에 맞는 H_K1
^eff 와 H_K2 를 얻을 수 있다. 그리고 이것들을 각각 계산하면 물질 고유의 자기 이방성 상수인 K₁ 과 K₂ 를 각각 구할 수 있다.
위에 설명한 방식이 바로 일반 석스미스-톰슨 방법이며, 이것은 자기 이방성을 평가하는 가장 일반적인 방법이다.
 
4. 기술개발 현황

현재 상용화되고 있는 MRAM은 대부분 스핀전달 토크를 이용하여 스위칭을 하는 방식을 채택하고 있다. 그러나 스핀궤도 토크를 이용하는 방식이 기존의 스핀전달토크를 이용하는 방식에 비하여 상대적으로 전력소모가 적고 메모리에서의 읽기와 쓰기가 다른 경로에서 일어나 읽기 작업 수행 시 간섭이 일어나지 않는다는 점에서 높은 평가받고 있어 스핀전달 토크를 스핀 궤도 토크로 대체하려는 시도들을 지속하고 있다.

그러나 현재 스핀궤도 토크를 이용하는 방식에도 외부 자기장을 필요로 한다거나, 적은 전류로 구동하기는 힘들다는 점, 그리고 열적 안정성이 떨어진다는 단점이 존재하기에 이러한 한계점을 극복하 려는 연구가 지속되고 있다.

이러한 문제를 해결하는 방식에는 여러 가지 방법이 제안이 되었는데 예를 들어 전력 효율성을 개선하기 위하여 전력 효율성이 좋으면서도 스핀궤도 결합을 강하게 하는 물질을 통해 스핀궤도 토크를 유도하는 방식이 제안 되었으며, 외부 자기장 없이 MRAM을 구동하기 위하여 기존에 강자성체를 이용하던 것과는 달리 반강자성체를 이용하여 교환 바이어스를 걸어주는 방식 등이 제안되었고 현재 제안된 방식 들을 기본 토대로 하여 활발한 MRAM 연구가 진행 중에 있다.

5. 결론

우리는 지금까지 MRAM을 구동하는 기술들과 그것의 성능을 어떻게 평가하는지에 대해서 알아보았다. 그리고 현재 그 기술들이 메모리에 어떤 식으로 적용되는지와 어떠한 한계점이 존재하고 이 한계점을 어떻게 개선하려고 하는지에 대해서도 살펴보았 다. 앞으로 메모리의 역할이 중요해지고 있는 4차 산업혁명 시대에 MRAM은 확실히 전도유망한 메모리이며, 그에 따라 MRAM 성능을 개선시키기 위한 연구는 지속되어져야 할 것이다.


침고문헌

[1] Inga Ennen, Daniel Kappe, Thomas Rempel, Claudia Glenske, and Andreas Hütten,. Sensors 2016, 16(6), 904
[2] S Yuasa and D D Djayaprawira, 2007 J. Phys. D: Appl. Phys. 40 R337
[3] Takayuki Nozaki, Tatsuya Yamamoto, Shinij Miwa, Masahito Tsujikawa, Masafumi Shirai, Shingi Yuasa, and Yoshishige Suzuki, Micromachines 2019, 10(5), 327
[4] Stuart S. P. Parkin, Masamitsu Hyashi, and Luc Thomas, SCIENCE 11 Apr 2008 Vol 320, Issue 5873 pp. 190-194
[5] Ung Hwan Pi, Kee Won Kim, Ji Young Bae, Sung Chul Lee, Young Jin Cho, Kwang Seok Kim, and Sunae Seo, Applied Physics Letters 97, 162507 (2010) 
[6] Jun Okabayashi, Yuki Iida, Qingyi Xiang, Hiroaki Sukegawa, and Seiji Mitani, Appl. Phys. Lett. 115, 252402 (2019) 
[7] Hyung Keun Gweon, Hyeon-Jong Park, Kyoung-Whan Kim, KyungJin Lee, and Sang Ho Lim, NPG Asia Materials volume 12, Article number: 23 (2020)