첨단 레이더 시스템은 100GHz 이상의 고주파 신호를 처리한다. 첨단 어레이 레이더 시스템은 디지털 신호 프로세싱을 이용해서 탐색, 식별, 추적, 목표물 설정, 감시 같은 다양한 기능 모드들이 가능하다. 대부분의 이러한 레이더 시스템은 기계식으로 작동하는 것이든 전자식으로 작동하는 것이든 상관없이 다중의 모드로 시스템 유연성을 향상시킬 수 있도록 하기 위해서 소프트웨어 지향적인 파형을 이용해서 신호를 디지털적으로 처리하고 있다. 이 글에서는 레이더 애플리케이션의 DSP(digital signal processing) 구현을 위해서 FPGA의 부동소수점 프로세싱을 이용할 때의 이점에 대해서 2회에 걸쳐 설명한다.

공간-시간 적응식 프로세싱

레이더 시스템들이 STAP(Space-Time Adaptive Processing) 같이 복잡하면서 프로세싱 속도가 높은 기법을 이용하는 일이 갈수록 늘어나고 있다. STAP는 레이더 애플리케이션에 이용되는 첨단의 신호 프로세싱 기법으로서, 공간과 시간 영역 모두에 작동해서 간섭을 억제한다.
이 기법은 클러터(clutter)나 재밍(jamming) 때문에 방해를 받는 경우에 느리게 움직이는 목표물을 탐지하는 것을 향상시킬 수 있으므로 심한 클러터 상황에서 느리게 움직이는 목표물을 탐색하는 것이 일상적인 경우의 공중 감시에 특히 적합하다. STAP의 해결 과제는 대기시간이 느리면 처리가 어렵다는 것이다. STAP 알고리즘을 실행할 때 FPGA를 이용하면 시스템 크기, 무게, 전력을 줄일 수 있을 뿐만 아니라 계산 대기시간을 낮출 수 있다.
STAP 알고리즘의 주된 요소는 QR 분해와 순방향 및 역방향 치환이다. QR 분해는 부동소수점 행렬 반전 연산이다. QR 분해와 치환 모두 고도로 반복적이며 수치 효과(numerical effects)에 민감하다. 레이더 시스템이 넓은 동적 범위를 요구하고 다른 SRAM FPGA와 멀티코어 프로세서는 고정소수점 프로세싱으로 반올림 잡음을 유발하므로, 부동소수점 프로세싱을 사용하는 것이 선호된다.

효과적인 레이더 시스템이 되기 위해서는 목표물과 잡음을 구분할 수 있어야 한다.
(그림 11)은 세 가지 잡음 유형을 보여준다. 리시버 잡음은 잡음 플로어로 작용하는 것으로서 이 그림에서 옅은 청색으로 표시된 것이다. 이 잡음 레벨은 안테나, 아날로그 프로세싱, 디지털 하향변환(DDC)을 포함하는 리시버 체인의 품질에 의해서 결정된다.
두 번째 잡음 요인은 클러터로서 녹색으로 표시된 것이다. 지상 클러터는 지상의 정지하고 있거나 느리게 움직이는 물체로부터의 반사를 기반으로 하는 것이다. 세 번째 잡음 요인은 재머(jammer)로부터 비롯되는 것이다. 재머는 통상적으로 모든 주파수에 걸쳐서 전달된다. 하지만 어느 한 재머는 오직 한 특정한 위치이므로 그림에서 황갈색으로 표시된 것과 같이 한 특정한 각도만 영향을 받는다.
STAP 프로세싱은 클러터와 재머를 필터링하고 억제함으로써 목표물을 좀더 수월하게 식별할 수 있도록 한다. STAP 프로세싱을 실시하기 위해서는 여러 가지 알고리즘이 가능하다. STAP 프로세싱 알고리즘을 선택할 때는 디자이너들이 전력 도메인으로 작동할 것인지 전압 도메인으로 작동할 것인지 결정해야 한다.
두 기법 모두 주변 레이더 셀들로부터 잡음 예상치를 도출하고 해당 셀로 이의 역을 적용해야 한다. 잡음 예상치의 역을 계산하기 위해서는 행렬 반전과 역 치환이 필요하다. 이와 같은 고도로 반복적인 연산은 오직 부동소수점 프로세싱을 이용해서만 가능하다.
뿐만 아니라 대량의 수학적 연산이 필요함으로써 많은 DSP는 데이터 프로세싱 성능이 부족할 수 있다. 이러한 제한점들이 첨단 레이더 애플리케이션 설계 시에 실제적으로 레이더 시스템의 잡음 억제 성능과 감도를 제한할 수 있다. 병렬 프로세싱 부동소수점 FPGA는 경쟁 시스템들에 비해서 뛰어난 잡음 억제 성능 및 감도를 달성할 수 있다.
STAP는 수행하기가 매우 까다로운 알고리즘이다. STAP를 이용할 때의 이점은 목표물 탐지 시에 감도를 크게 향상시킬 수 있다는 것이다. 이를 달성하기 위해서는 매우 높은 프로세싱 성능, 낮은 지연시간, 신속한 적응, 매우 높은 동적 범위가 요구된다.

FPGA를 이용한 STAP 프로세싱

알테라는 Stratix 시리즈 FPGA를 이용해서 이 알고리즘을 어떻게 구현할 수 있는지 보여주기 위해서 STAP 레이더 부동소수점 디자인 예를 개발했다. 이 디자인 예는 고성능 부동소수점 및 벡터 프로세싱을 어떻게 구현할 수 있는지 잘 보여준다.

알테라는 효율적인 STAP 부동소수점 프로세싱을 구현할 수 있도록 다음을 지원한다.
- 토대 실리콘 구조가 지원하는 부동소수점 연산
- 디자이너들이 이용할 수 있도록 효율적인 부동소수점 라이브러리 제공
- 알고리즘을 실리콘 구조로 효율적으로 맵핑할 수 있는 설계 입력 툴
이 STAP 디자인 예는 알테라의 부동소수점 지원을 잘 보여준다. 이 디자인 예는 16개 안테나, 16개 도플러 빈, 64개 목표물 스티어링 벡터, 1kHz의 펄스 반복 주파수를 포함해서, 실제적인 조합의 파라미터들로 이루어진 것이다.
프로세싱 속도는 80 GFLOP/s 이다. EP4SGX230 중간 수준 밀도 Stratix IV FPGA를 이용해서 이 전체적인 디자인 예를 구현할 수 있다. 또 MATLAB 및 DSP Builder advanced blockset을 이용해서 작성하였다.

이는 다음 단계들로 이루어진 표준적인 설계 플로우이다.
1. MATLAB으로 스티뮬러스 생성과 결과 플로팅 기능을 포함한 전체적인 STAP 프로세싱 체인을 구현한다.
2. DSP Builder advanced blockset을 이용해서 데이터 프로세싱 체인을 구현한다.
3. MATLAB/DSP Builder 동시 시뮬레이션을 실시해서 제대로 작동하는지 검증한다.

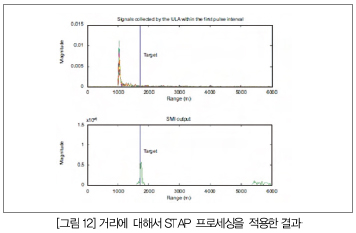
(그림 12)는 이 디자인 예를 이용해서 작성된 플롯을 보여준다. 상단 플롯은 STAP를 적용하기 전에 ULA(Uniform Linear Array)가 수집한 신호를 보여준다. 파란색 선은 목표물의 위치를 보여준다. 이 플롯에서는 재머가 시스템을 완전히 압도하고 있으므로 목표물을 인식할 수 없다는 것을 알 수 있다.
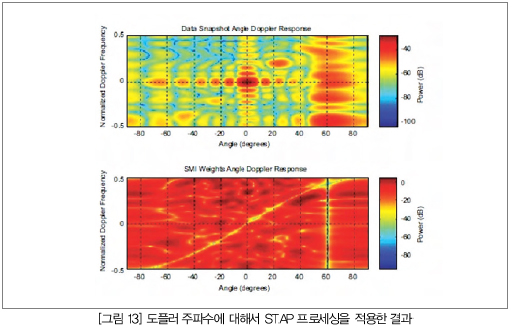
(그림 13)은 데이터 스냅 샷으로서 60도에서 재머가 압도적으로 자리잡고 있다. 두 번째 플롯에서는 STAP로 계산한 가중치를 보여준다. 이 그림에서는 60도에서 -80dB 가중치를 적용함으로써 재머를 억제하는 것을 알 수 있다. 클러터를 따라서 노란색 선은 -30dB ~ -40dB의 가중치로 클러터를 억제하고 있는 것을 보여준다.
(그림 13)에서 재머를 억제하고 있는 위치가 정확하게 (그림 11)에서 재머가 표시된 곳이다. (그림 11)에서 녹색 대각선으로 표시된 클러터는 (그림 13)의 두 번째 플롯에서 노란색 클러터 억제와 일치한다.
(그림 13)에서는 알테라 Stratix IV FPGA를 이용함으로써 부동소수점 프로세싱을 이용해서 높은 동적 범위가 가능해짐으로써 목표물 탐지에 있어서 감도가 크게 향상된다는 것을 알 수 있다. Stratix 시리즈 디바이스를 이용해서 구현하는 레이더 시스템은 증가된 임베디드 메모리와 DSP 소자 밀도로 병렬 프로세싱이 가능함으로써 지연시간이 낮고 환경 변화에 빠르게 적응할 수 있다.
요약적으로 말해서 알테라의 STAP 디자인 예는 복잡한 알고리즘을 어떻게 실제 하드웨어로 구현할 수 있는지 잘 보여주는 예이다. 이 예는 Simulink 설계 입력 기법을 이용해서 토대 실리콘 구조의 가능성을 최대한 활용할 수 있도록 한다. 이 기법을 이용함으로써 레이더 시스템 디자이너들은 단일 FPGA로 수백 GFLOP을 달성할 수 있으므로 레이더 시스템 성능을 한 차원 향상시킬 수 있을 것이다.

기타 프로세싱 알고리즘

레이더 개발자들은 그 밖에도 여러 알고리즘에 관심을 가지고 있다. CFAR
(Constant False Alarm Rate) 프로세싱은 대부분의 경우에 프로세싱 시에 이루어지는 최초의 탐지 의사결정이다.
이 알고리즘은 인접 셀들의 잡음을 적응식으로 측정하고 탐지 임계값을 적응식으로 조절한다. CFAR은 잡음이 존재하는 상황에서도 허위 경보의 확률을 일정한 수준으로 유지할 수 있다. 디자이너들은 부동소수점과 CFAR 알고리즘을 함께 이용함으로써 잠수함 잠망경이 거친 파도 때문에 방해를 받는 경우와 같이, 백그라운 클러터로 둘러싸인 목표물을 탐지할 수 있다.
또 다른 기법으로서 펄스 압축은 트랜스미터 전력을 낮추면서 원하는 거리 해상도를 유지한다. 디자이너들은 부동소수점 FFT를 이용해서 시스템의 필터링 성능을 향상시킬 수 있다.



도플러 필터링은 도플러 효과(Doppler Effect)를 이용해서 회신 펄스와 발신 펄스의 주파수 차이를 비교한다. FFT 필터가 레이더를 향한 목표물 속도 벡터를 빈(bin)으로 정렬한다. 이 경우에 또한 부동소수점 프로세싱을 이용해서 이 계산의 감도를 향상시킬 수 있다.
(표 2)와 (표 3)은 알테라 부동소수점 FFT IP 코어의 벤치마크 결과를 보여준다. 이 IP 코어는 진정한 부동소수점 형식을 구현함으로써 숫자 블록을 스케일링하거나 반올림 오류를 일으키지 않고서 각각의 개별 숫자를 스케일링한다.
(표 2)는 Quartus II 소프트웨어 버전 10.1을 이용해서 Stratix IV 4SGX70 디바이스의 단일 1024 포인트 부동소수점 FFT 코어의 자원 및 성능 결과를 보여준다. (표 3)은 Stratix IV 4SGX530 디바이스의 14개 1024 포인트 FFT IP 코어의 자원 및 성능 결과이다.
이들 결과를 보면 고밀한 대형 부동소수점 디자인이라 하더라도 300MHz 이상으로 클로킹한다는 것을 알 수 있다. 이러한 결과는 FFT IP 코어를 이용해서 쉽게 반복할 수 있다.

알테라의 부동소수점 FPGA

시스템으로 부동소수점 프로세싱을 구현하기 위해서는 다음과 같은 요소들이 필요하다:
- 부동소수점 프로세싱을 지원하는 실리콘 구조
- 부동소수점 가능 툴
- 효율적인 부동소수점 함수들을 포함하는 포괄적인 라이브러리

최근까지만 해도 대다수 실리콘, 툴, IP가 통합되어 있지 않았으며 디자이너들이 모든 요소들을 합쳐야 했다. 알테라 FPGA는 블록 절단형(truncated) 부동소수점 계산이 아니라 진정한 부동소수점 계산을 처리한다는 점에서 시장의 어느 앞선 FPGA보다 뛰어나다.
또한 알테라는 뛰어난 실리콘 아키텍처를 지원할 수 있는 툴 플로우 및 IP 라이브러리를 설계했다. 알테라 FPGA는 또한 FPGA의 자연스러운 병렬성을 활용한다는 점에서 부동소수점 프로세싱을 위해서 마이크로프로세서 및 디지털 신호 프로세서보다 우수하다.
알테라 FPGA는 마이크로프로세서와 달리 수천 개의 고정밀도 하드구현 곱셈기 회로를 포함함으로써 이것을 가수부 곱셈에 이용하거나 고속 배럴 쉬프터(barrel shifter)로 이용할 수 있다. 가수부 소수점을 정하기 위한 정규화를 실시하기 위해서는 데이터 쉬프팅이 필요하며, 지수부를 정렬하기 위해서는 가수부 역정규화가 필요하다.
단순한 배럴 쉬프터 구조를 이용해서 이 작업을 수행하기 위해서는 각각의 비트 위치에 대해서 매우 높은 fan-in 다중화기와 각각의 가능한 비트 입력을 연결하기 위한 루팅이 필요하다. 알테라 디바이스는 경쟁 FPGA에서 디바이스 자원 제약, 클록 레이트 저하, 과도한 로직 사용을 야기하는 높은 fan-in 및 루팅 문제를 해결할 수 있도록 최적화되었다.
알테라 FPGA는 IEEE 754 표현보다 더 긴 가수부를 이용할 수 있다. 이것은 가변 정밀도 DSP 블록이 27x27 및 36x36 곱셈기 크기를 지원하기 때문에 가능한 것으로서 이러한 곱셈기 크기를 23비트 단정도 부동소수점 데이터패스에 이용할 수 있다.
구성 가능 로직을 이용함으로써 필요에 따라서 부동소수점 가수부 정밀도를 확장할 수 있으며, 그러면서 또한 IEEE 754 호환 인터페이스를 유지할 수 있다. 23비트 대신에 27비트 같은 추가 비트의 가수부 크기를 이용함으로써 한 연산에서 다음 연산으로 넘어가면서 추가적인 정밀도가 가능할 수 있으며 좀 더 효율적인 하드웨어를 구현할 수 있다.
예를 들어서 완벽한 병렬 벡터 도트 곱 연산을 위해서는 부동소수점 곱셈기 뱅크에 이어서 부동소수점 덧셈기로 이루어진 덧셈기 트리가 필요하다. 추가적인 가수부 정밀도를 이용함으로써 덧셈기 트리의 입구 및 출구 스테이지를 제외하고는 부동소수점 덧셈기와 관련된 로직 집중적 역정규화 및 정규화 함수를 제거할 수 있다.

28nm 가변 정밀도 아키텍처

28nm Stratix V 및 Arria V FPGA의 DSP 블록은 차세대 레이더 및 전자전(electronic warfare) 시스템의 요구를 충족할 수 있도록 설계되었다. 알테라의 새로운 가변 정밀도 DSP 아키텍처를 이용하면 디자이너들이 디자인의 각 부분에 대해서 필요한 정밀도를 지정할 수 있다. 그럼으로써 로직과 DSP 자원을 좀더 효율적으로 활용할 수 있고 전력 소비를 낮출 수 있으며 필요한 곳에서 더 높은 정밀도의 DSP를 구현할 수 있다.
18비트 정밀도 모드이면 가변 정밀도 아키텍처가 듀얼 18x18 곱셈기를 포함하며 선택적으로 하드 전치 덧셈기를 이용할 수 있다. 전치 덧셈기는 샘플들을 추가하고 동일한 계수로 곱셈을 할 수 있으므로 대칭 필터링 같은 애플리케이션에 유용하다.
18x18 모드는 가변 정밀도가 듀얼 통합 계수 레지스터 뱅크를 지원하며 직접 형식 및 시스톨릭 형식 FIR 필터를 효율적으로 구현할 수 있다. 또한 FFT 구현을 위해서 필수적인 요소로서 효율적인 복소수 곱셈을 지원한다.
비대칭적 크기 곱셈기는 FFT 프로세싱에 이용되는 복소수 곱셈에 유용하다. 이것은 복소수 회전 인수(twiddle factor)에 대해서 고정 정밀도 계수를 제공하며 프로세싱 시에 발생하는 데이터 증가를 허용하기 때문이다. FFT에서는 매 radix2 스테이지마다 1비트 속도로 데이터 증가가 발생한다.
Stratix V 가변 정밀도 DSP 블록은 FFT 프로세싱에 적합하도록 설계되었다. 2개 DSP 블록이 18x18 복소수 곱셈기를 실행하고, 3개 DSP 블록이 18x25 복소수 곱셈기를 실행하고, 4개 DSP 블록이 18x36 복소수 곱셈기를 실행할 수 있다. 그러므로 곱셈기의 데이터의 비트 정밀도 증가에 비례하게 DSP 자원을 늘릴 수 있으며 고정 정밀도 18비트 회전 인수를 이용할 수 있다.
그러므로 디자이너들이 FFT의 각 radix 단계에서 정밀도와 DSP 블록 자원의 사용 및 그에 따른 전력 소비를 절충할 수 있으므로 DSP 자원을 고도로 효율적으로 사용할 수 있다. 이들 모드를 이용함으로써 가변 정밀도 DSP 아키텍처는 대형 안테나 어레이로부터 들어오는 데이터의 병렬 주파수 도메인 프로세싱을 수행하기에 매우 적합하다.
뿐만 아니라 가변 정밀도 DSP 블록은 18비트 또는 27비트 모드로 최초로 내부 계수 저장 뱅크를 포함한다. 그럼으로써 외부 메모리 블록의 사용과 필요한 계수 루팅을 감소시킨다. 그럼으로써 또한 높은 클록 레이트로 타이밍 종결을 향상시킨다.



가변 정밀도 DSP는 또한 고유의 27x27 곱셈기에 업계에서 가장 큰 것으로서 64비트 누산기를 지원한다. 그러므로 더 높은 정밀도로 더 높은 동적 범위의 신호 프로세싱이 가능하므로 고정소수점 수치 프로세싱을 줄일 수 있다. 또한 27비트 모드로 하드 전치 덧셈기, 통합적 계수 레지스터 뱅크, 직접 형식 또는 시스톨릭 형식 FIR 필터를 지원한다.
뿐만 아니라 가변 정밀도 DSP 블록으로 18x18 및 27x27 곱셈기를 결합함으로써 더 대형의 곱셈기 크기를 지원할 수 있다. 이 기법은 36x36 및 54x54 곱셈기 크기의 고성능 구현이 가능하다. 27x27, 36x36, 54x54 곱셈기 크기는 단정도, 단정도 확장, 배정도 부동소수점을 효율적으로 구현할 수 있다.

융합적 데이터패스 툴 플로우

알테라의 고성능 저-지연 부동소수점 툴 플로우를 (그림 14)에서 설명한 바와 같이 ‘융합적 데이터패스(fused datapath)’ 기술이라고 한다.
이 툴 플로우를 이용하면 혼합적인 고정소수점 및 부동소수점 FPGA 벡터 신호 프로세싱 데이터패스를 구현할 수 있다. 이 툴이 정규화 요구를 분석하고 필요한 곳에만 이들 스테이지를 삽입한다. 이 기법은 로직, 루팅, 곱셈기 기반 쉬프팅 자원을 크게 줄일 수 있다. 이 기법은 또한 매우 규모가 큰 부동소수점 디자인이라 하더라도 훨씬 더 높은 fMAX 또는 클록 레이트를 달성할 수 있다.



부동소수점 표준을 준수하기 위해서는 IEEE 754 표현이 필요하므로 FFT(fast Fourier transform), 행렬 반전, 사인 함수, 맞춤형 데이터패스에 상관없이 모든 부동소수점 함수들은 각 함수의 경계에서 이 인터페이스를 지원한다.
융합적 데이터패스 툴 플로우는 IEEE 754 마이크로프로세서 기법과 다른 결과를 낼 가능성이 있다. 이러한 차이가 나는 가장 큰 이유는 부동소수점 연산은 결합적(associative)이지 않기 때문이다.
동일한 집합의 숫자들을 역순으로 합했을 때는 LSB(least significant bit)가 다양하게 나올 수 있다. 융합적 데이터패스 기법을 검증하기 위해서는 디자이너가 융합적 데이터패스 툴을 이용해서 허용오차를 선언하고 융합적 데이터패스 툴 플로우로부터 출력된 하드웨어 결과를 시뮬레이션 모델 결과와 비교한다.
알테라는 융합적 데이터패스 방법론의 산술 정밀도를 분석한 결과 IEEE 754보다 통계적으로 더 정확한 것으로 나타났다. 이 융합적 데이터패스 툴 플로우는 알테라의 DSP Builder advanced blockset에 통합되어 있으며, 매스웍스의 MATLAB 및 Simulink에서 지원한다. 이 기법은 편리하게 시뮬레이션이 가능할 뿐만 아니라 혼합적인 고정소수점 및 부동소수점 디자인을 FPGA로 구현할 수 있도록 한다.
(그림 15)는 어떻게 부동소수점 복소수 타입(단정도 및 배정도 아키텍처)을 고정소수점 타입과 함께 이용하고 있는지 보여준다. DSP Builder를 이용하면 단일 환경으로 혼합적인 부동소수점 및 고정소수점 디자인을 구현할 수 있다. 이 툴은 또한 복소수 숫자 및 벡터의 추상화가 가능하므로 디자인 기술을 명료하게 하고 변경하기 수월하게 한다. 가수부, 지수부, 정규화, 특수 조건들에 관련된 복잡성을 부동소수점 소프트웨어 툴과 마찬가지로 추상화할 수 있다.

부동소수점 함수 라이브러리

Math.h 함수들은 간단한 C 라이브러리로 제공할 예정인 간단한 함수들이다(trigonometric, log, expo
nent, inverse square root, 그리고 divide 같은 기본적 연산자). 융합적 데이터패스 플로우를 위해서 이러한 함수들을 부동소수점 라이브러리로 지원한다.

높은 동적 범위를 필요로 하는 가장 일반적인 함수 중의 하나가 행렬 반전이다. 이를 위해서 융합적 데이터패스 라이브러리가 다음과 같은 참조 디자인을 포함함으로써 선형 대수를 지원한다.
- 행렬 곱셈
- Cholesky 분해(행렬 반전 알고리즘에 이용)
- LU 분해(행렬 반전 알고리즘에 이용)
- QR 분해(행렬 발전 알고리즘에 이용)

DSP Builder 툴 플로우는 복소수 및 벡터 표현을 지원한다. 또한 동일한 디자인으로 고정소수점 및 부동소수점 연산을 편리하게 혼합할 수 있다. 이 점은 차세대 레이더 시스템에 이용되는 여러 알고리즘의 다수의 선형 대수 연산자를 효율적으로 구현하기 위해서 필수적인 것이다.
그럼으로써 또한 신속하게 디자인을 재사용하고 벡터 및 행렬 크기를 변경할 수 있다. 끝으로는, 융합적 데이터패스 툴 플로우를 위해서 포괄적인 라이브러리를 지원하므로 고객들이 대형의 복잡하고 고도로 최적화된 부동소수점 데이터패스를 구현할 수 있다.